The Nationwide Inpatient Sample (NIS) of the Healthcare Cost and Utilization Project (HCUP) was developed to provide analyses of hospital utilization, charges and quality of care across the United States. The target universe includes all acute-care discharges from all community hospitals in the United States; the NIS comprises all discharges from a sample of hospitals in this target universe. NIS 1998 includes data for calendar year 1998. Previous years covered 1988 through 1997.
| Calendar Year | States | Sample Hospitals | Sample Discharges (Millions) |
|---|---|---|---|
| 1988–1992 | 8–11 | 758–875 | 5.2–6.2 |
| 1993 | 17 | 913 | 6.5 |
| 1994 | 17 | 904 | 6.4 |
| 1995 | 19 | 938 | 6.7 |
| 1996 | 19 | 906 | 6.5 |
| 1997 | 22 | 1012 | 7.1 |
| 1998 | 22 | 984 | 6.8 |
Potential research issues focus on both discharge- and hospital-level outcomes. Discharge outcomes of interest include trends in inpatient treatments with respect to:
Hospital outcomes of interest include:
These and other outcomes are of interest for the nation as a whole and for policy-relevant inpatient subgroups defined by geographic regions, patient demographics, hospital characteristics, physician characteristics, and pay sources.
This report provides a detailed description of the NIS 1998 sample design, as well as a summary of the resultant hospital sample. Sample weights were developed to obtain national estimates of hospital and inpatient parameters. These weights and other special-use weights are described in detail. Tables include cumulative information for all previous NIS releases to provide a longitudinal view of the database.
The hospital universe is defined by all hospitals located in the U.S. that were open during any part of the calendar year and were designated as community hospitals in the American Hospital Association (AHA) Annual Survey of Hospitals. For purposes of the NIS, the definition of a community hospital is that used by the AHA: "all nonfederal short-term general and other specialty hospitals, excluding hospital units of institutions." Consequently, Veterans Hospitals and other federal hospitals (Department of Defense and Indian Health Service) are excluded. Beginning in 1998, rehabilitation hospitals were excluded from the NIS hospital universe because the type of care provided, and the characteristics of the discharges from these hospitals, were markedly different from other short-term hospitals. Table 1 shows the number of universe hospitals for each year based on the AHA Annual Survey. It can be seen that the number of hospitals has decreased in 1998. This is partly due to the elimination of rehabilitation hospitals from the NIS 1998 universe.
| Year | Number of Hospitals |
|---|---|
| 1988 | 5,607 |
| 1989 | 5,548 |
| 1990 | 5,468 |
| 1991 | 5,412 |
| 1992 | 5,334 |
| 1993 | 5,313 |
| 1994 | 5,290 |
| 1995 | 5,260 |
| 1996 | 5,182 |
| 1997 | 5,113 |
| 1998 | 4,915 |
All U.S. hospital entities that were designated community hospitals in the AHA hospital file, except rehabilitation hospitals, were included in the hospital universe. Therefore, if two or more community hospitals merged to create a new community hospital, the original hospitals and the newly formed hospital were all considered separate hospital entities in the universe for the year of the merge. Likewise, if a community hospital split, the original hospital and all newly created community hospitals were separate entities in the universe for the year of the split. Finally, community hospitals that closed during a year were included as long as they were in operation during some part of the calendar year.
The NIS sampling strata were defined based on five hospital characteristics contained in the AHA hospital files. In order to improve the representativeness of the NIS, given the expansion of the number of contributing states, the sampling and weighting strategy was evaluated and revised for the 1998 NIS. This included changes to the definitions of the strata variables. A full description of this process can be found in the report Changes in NIS Sampling and Weighting Strategy for 1998, which will be available later in 2001. A description of the sampling procedures and definitions of strata variables used from 1988 through 1997 can be found in the report: Design of the HCUP Nationwide Inpatient Sample, Release 6. For the 1998 NIS, the stratification variables were defined as follows:
| Location and Teaching Status | Hospital Bed Size | ||
|---|---|---|---|
| Small | Medium | Large | |
| NORTHEAST | |||
| Rural | 1-49 | 50-99 | 100+ |
| Urban, non-teaching | 1-124 | 125-199 | 200+ |
| Urban, teaching | 1-249 | 250-424 | 425+ |
| MIDWEST | |||
| Rural | 1-29 | 30-49 | 50+ |
| Urban, non-teaching | 1-74 | 75-174 | 175+ |
| Urban, teaching | 1-249 | 250-374 | 375+ |
| SOUTH | |||
| Rural | 1-39 | 40-74 | 75+ |
| Urban, non-teaching | 1-99 | 100-199 | 200+ |
| Urban, teaching | 1-249 | 250-449 | 450+ |
| WEST | |||
| Rural | 1-24 | 25-44 | 45+ |
| Urban, non-teaching | 1-99 | 100-174 | 175+ |
| Urban, teaching | 1-199 | 200-324 | 325+ |
The bed size cutoff points were chosen so that approximately one-third of the hospitals in a given region, location and teaching status combination would be in each bed size category (small, medium or large). Different cutoff points for rural, urban non-teaching, and urban teaching hospitals were used because hospitals in those categories tend to be small, medium, and large, respectively. For example, a medium-sized teaching hospital would be considered a rather large rural hospital. Further, the size distribution is different among regions for each of the urban/teaching categories. For example, teaching hospitals tend to be smaller in the West than they are in the South. Using differing cutoff points in this manner avoids strata with small numbers of hospitals in them.
Rural hospitals were not split according to teaching status, because rural teaching hospitals were rare. For example, in 1998 there were only 56 rural teaching hospitals, slightly over 1% of the total hospital universe. The bed size categories were defined within location and teaching status because they would otherwise have been redundant. Rural hospitals tend to be small; urban non-teaching hospitals tend to be medium-sized; and urban teaching hospitals tend to be large. Yet it was important to recognize gradations of size within these types of hospitals. For example, in serving rural discharges, the role of "large" rural hospitals (particularly rural referral centers) often differs from the role of "small" rural hospitals.
To further ensure geographic representativeness, implicit stratification variables included state and three-digit zip code (the first three digits of the hospital's five-digit zip code). The hospitals were sorted according to these variables prior to systematic random sampling.
The universe of hospitals was established as all community hospitals located in the U.S. with the exception, beginning in 1998, of rehabilitation hospitals. However, it was not feasible to obtain and process all-payer discharge data from a random sample of the entire universe of hospitals because it would have been too costly to obtain data from individual hospitals, and it would have been too burdensome to process each hospital's unique data structure.
Therefore, the NIS sampling frame was constructed from the subset of universe hospitals that released their discharge data for research use. Two sources for all-payer discharge data were state agencies and private data organizations, primarily state hospital associations. At the time the 1998 sample was drawn, the Agency for Healthcare Research and Quality (AHRQ) had agreements with 22 data sources that maintain statewide, all-payer discharge data files to include their data in the HCUP database. Prior years of HCUP included fewer states, as shown in Table 3.
| Years | States in the Frame |
|---|---|
| 1988 | California, Colorado, Florida, Iowa, Illinois, Massachusetts, New Jersey, and Washington |
| 1989-1992 | Add Arizona, Pennsylvania, and Wisconsin |
| 1993 | Add Connecticut, Kansas, Maryland, New York, Oregon, South Carolina |
| 1994 | No new additions |
| 1995 | Add Missouri, Tennessee |
| 1996 | No new additions |
| 1997 | Add Georgia, Hawaii, and Utah |
| 1998 | No new additions |
The list of the entire frame of hospitals was composed of all AHA community hospitals in each of the frame states that could be matched to the discharge data provided to HCUP. If an AHA community hospital could not be matched to the discharge data provided by the data source, it was eliminated from the sampling frame (but not from the target universe). Further restrictions were put on the sampling frames for Georgia, Hawaii, Illinois, South Carolina, Missouri, and Tennessee.
The Illinois Health Care Cost Containment Council stipulated that no more than 40 percent of the discharges provided by Illinois could be included in the database for any calendar quarter. Consequently, a systematic random sample of 72 percent of Illinois hospitals was drawn for the 1998 frame. This prevented the sample from including more than 40 percent of Illinois discharges.
Georgia, Hawaii, South Carolina and Tennessee stipulated that only hospitals that appear in sampling strata with two or more hospitals from the state were to be included in the NIS. Due to this restriction, four Hawaii hospitals, four South Carolina hospitals and one Tennessee hospital were excluded from the 1998 frame. All hospitals from Georgia were in strata with at least two hospitals, and thus all remained in the sampling frame. Two additional South Carolina hospitals, although in sampling strata with other hospitals, were removed from the sampling frame due to unique characteristics that would make them identifiable. After these restrictions were applied, the 1998 sampling frame included 154 Georgia hospitals, 13 Hawaii hospitals, 54 South Carolina hospitals and 105 Tennessee hospitals.
Missouri stipulated that only hospitals that had signed releases for public use should be included in the NIS. For 1998, thirty-four Missouri hospitals signed releases for confidential use only. These hospitals were excluded from the sampling frame, leaving 75 hospitals in the 1998 frame.
The number of frame hospitals for each year is shown in Table 4.
| Year | Number of Hospitals |
|---|---|
| 1988 | 1,247 |
| 1989 | 1,658 |
| 1990 | 1,620 |
| 1991 | 1,604 |
| 1992 | 1,591 |
| 1993 | 2,168 |
| 1994 | 2,135 |
| 1995 | 2,284 |
| 1996 | 2,268 |
| 1997 | 2,452 |
| 1998 | 2,438 |
The NIS is a stratified probability sample of hospitals in the frame, with sampling probabilities calculated to select 20 percent of the universe contained in each stratum. The overall objective was to select a sample of hospitals generalizable to the target universe, which includes hospitals outside the frame (i.e., having zero probability of selection). Moreover, this sample was to be geographically dispersed, yet drawn from the subset of states with inpatient discharge data that agreed to provide such data to the project.
It should be possible, for example, to estimate DRG-specific average lengths of stay over all U.S. hospitals using weighted average lengths of stay, based on averages or regression estimates from the NIS. Ideally, relationships among outcomes and their correlates estimated from the NIS should generally hold across all U.S. hospitals. However, since only 22 states contributed data to this 1998 release, some estimates may differ from estimates from comparative data sources. When possible, estimates based on the NIS should be checked against national benchmarks, such as Medicare data or data from the National Hospital Discharge Survey to determine the appropriateness of the NIS for specific analyses.
The target sample size was 20 percent of the total number of community hospitals in the U.S. for 1998. This sample size was determined by AHRQ based on their experience with similar research databases.
Alternative stratified sampling allocation schemes were considered. However, allocation proportional to the number of hospitals is preferred for several reasons:
Once the universe of hospitals was stratified, up to 20 percent of the total number of U.S. hospitals was randomly selected within each stratum. If too few frame hospitals were in the stratum, then all frame hospitals were selected for the NIS, subject to sampling restrictions specified by states. To simplify variance calculations, at least two hospitals were drawn from each stratum. If fewer than two frame hospitals were contained in a stratum, then that stratum was merged with an "adjacent" stratum containing hospitals with similar characteristics.
A systematic random sample was drawn from each stratum, after sorting hospitals by state within each stratum, then by the three-digit zip code (the first three digits of the hospital's five-digit zip code) within each state, and then by a random number within each three-digit zip code. These sorts ensured further geographic generalizability of hospitals within the frame states, and random ordering of hospitals within three-digit zip codes.
Generally, three-digit zip codes that are near in value are geographically near within a state. Furthermore, the U.S. Postal Service locates regional mail distribution centers at the three-digit level. Thus, the boundaries tend to be a compromise between geographic size and population size.
Two nonoverlapping 10 percent subsamples of discharges were drawn from the NIS file for each year. +The subsamples were selected by drawing every tenth discharge starting with two different starting points (randomly selected between 1 and 10). Having a different starting point for each of the two subsamples guaranteed that they would not overlap. Discharges were sampled so that 10 percent of each hospital's discharges in each quarter were selected for each of the subsamples. The two samples can be combined to form a single, generalizable 20 percent subsample of discharges.
Using the current 1998 NIS procedures, all frame hospitals within a stratum have an equal probability of selection for the sample, regardless of whether they had been in prior NIS samples. This deviates from the procedure used for earlier samples, which maximized the longitudinal component of the NIS series.
Further description of the sampling procedures for earlier releases of the NIS can be found in the report: Design of the HCUP Nationwide Inpatient Sample, Release 6. For a description of the development of the new 1998 NIS sample design, see the report: Changes in NIS Sampling and Weighting Strategy for 1998.
Beginning in 1993, the NIS samples contain no zero-weight hospitals. For a description of zero-weight hospitals in the 1998-1992 sample, see the report: Design of the HCUP Nationwide Inpatient Sample, Release 1.
The annual numbers of hospitals and discharges in each release of the NIS are shown in Table 5. For the 1988-1992 NIS, zero-weight hospitals were maintained to provide a longitudinal sample, so figures are presented for both the regular NIS sample and the total sample.
| Regular Sample | Total Sample | |||
|---|---|---|---|---|
| Year | Number of Hospitals | Number of Discharges | Number of Hospitals | Number of Discharges |
| 1988 | 758 | 5,242,904 | 759 | 5,265,756 |
| 1989 | 875 | 6,067,667 | 882 | 6,110,064 |
| 1990 | 861 | 6,156,638 | 871 | 6,268,515 |
| 1991 | 847 | 5,984,270 | 859 | 6,156,188 |
| 1992 | 838 | 6,008,001 | 856 | 6,195,744 |
| 1993 | 913 | 6,538,976 | - | - |
| 1994 | 904 | 6,385,011 | - | - |
| 1995 | 938 | 6,714,935 | - | - |
| 1996 | 906 | 6,542,069 | - | - |
| 1997 | 1,012 | 7,148,420 | - | - |
| 1998 | 984 | 6,827,350 | - | - |
A breakdown of the 1998 NIS hospital sample by geographic region is shown in Table 6. For each geographic region, Table 6 shows the number of:
| Hospital Region | Universe | Frame | % of Universe in Frame | Target | Sample | Shortfall |
|---|---|---|---|---|---|---|
| Northeast | 690 | 588 | 85.2% | 138 | 140 | -2 |
| Midwest | 1,428 | 579 | 40.5% | 286 | 290 | -4 |
| South | 1,870 | 557 | 29.8% | 374 | 361 | 13 |
| West | 927 | 714 | 77.0% | 185 | 193 | -8 |
| Total | 4,915 | 2,438 | 49.6% | 983 | 984 | -1 |
For example, in 1998 the Northeast region contained 690 hospitals in the universe. It also contained 588 hospitals in the frame, of which 140 hospitals were drawn for the sample. This was two more than the target sample size of 138 hospitals. In the south, there was a shortfall of 13 hospitals indicating that the frame did not provide an adequate number of hospitals to reach the target sample size.
Table 7 shows the number of hospitals in the universe, frame, and regular sample for each state in the sampling frame for 1998. The difference between the universe and the frame represents the difference in the number of community hospitals in the 1998 AHA Annual Survey of Hospitals and the number of community hospitals for which data were supplied to HCUP in all states except Illinois, Hawaii, South Carolina, Tennessee and Missouri.
The number of hospitals in the Missouri frame is 48 less than the Missouri universe. Thirty-four hospitals were excluded because they signed release for confidential use only, and 14 hospitals identified in AHA data were not included in the data supplied to HCUP.
| State | Hospital Universe | Frame Size | Sample |
|---|---|---|---|
| AZ | 61 | 59 | 14 |
| CA | 401 | 393 | 97 |
| CO | 67 | 66 | 20 |
| CT | 32 | 31 | 7 |
| FL | 197 | 194 | 109 |
| GA | 154 | 154 | 114 |
| HI | 20 | 13 | 4 |
| IA | 116 | 116 | 53 |
| IL | 201 | 145 | 75 |
| KS | 128 | 121 | 56 |
| MA | 74 | 70 | 17 |
| MD | 50 | 50 | 32 |
| MO | 123 | 75 | 39 |
| NJ | 78 | 77 | 17 |
| NY | 219 | 218 | 52 |
| OR | 60 | 59 | 18 |
| PA | 198 | 192 | 47 |
| SC | 63 | 54 | 34 |
| TN | 116 | 105 | 72 |
| UT | 41 | 40 | 16 |
| WA | 85 | 84 | 24 |
| WI | 122 | 122 | 67 |
| TOTAL | 2,606 | 2,438 | 984 |
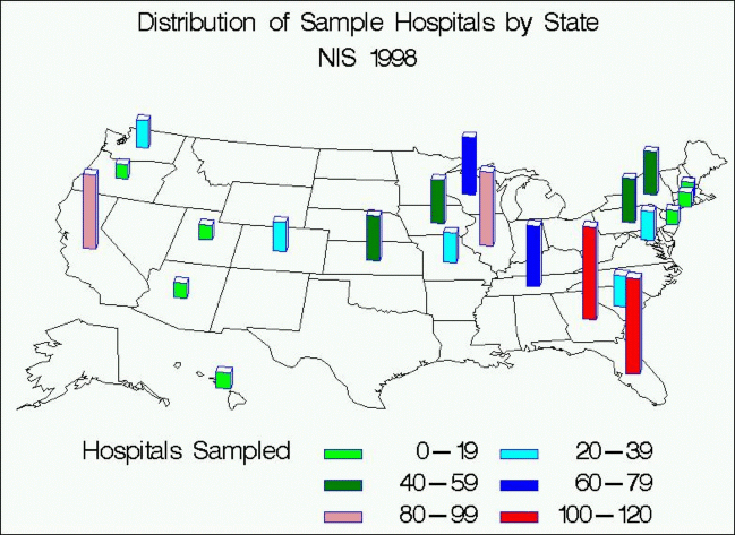
It can be seen from the map above that hospitals were sampled throughout each region of the United States. The impact of stratification can be seen as well. In those regions where a higher proportion of states are represented (the northeast and west) relatively fewer hospitals are sampled from each state than in regions where fewer states are included. The number of hospitals and discharges by state and region are given in Table 8 below.
| REGION | State | Number Hospitals in Sample | Number Discharges in Sample |
|---|---|---|---|
| Midwest | Iowa | 53 | 162,249 |
| Illinois | 75 | 611,251 | |
| Kansas | 56 | 148,770 | |
| Missouri | 39 | 221,087 | |
| Wisconsin | 67 | 363,740 | |
| Northeast | Connecticut | 7 | 49,372 |
| Massachusetts | 17 | 193,383 | |
| New Jersey | 17 | 262,629 | |
| New York | 52 | 470,444 | |
| Pennsylvania | 47 | 355,476 | |
| South | Florida | 109 | 1,026,428 |
| Georgia | 114 | 532,539 | |
| Maryland | 32 | 367,623 | |
| South Carolina | 34 | 217,642 | |
| Tennessee | 72 | 479,830 | |
| West | Arizona | 14 | 108,806 |
| California | 97 | 841,691 | |
| Colorado | 20 | 130,392 | |
| Hawaii | 4 | 23,962 | |
| Oregon | 18 | 70,600 | |
| Utah | 16 | 58,586 | |
| Washington | 24 | 130,750 | |
| Total | 984 | 6,827,350 |
Although the sampling design was simple and straightforward, it is necessary to incorporate sample weights to obtain state and national estimates. Therefore, sample weights were developed separately for hospital- and discharge-level analyses. Hospital-level weights were developed to weight NIS sample hospitals to the hospital universe. Similarly, discharge-level weights were developed to weight NIS sample discharges to the hospital universe.
Hospital weights to the universe were calculated by post-stratification. For each year, hospitals were stratified on the same variables that were used for sampling: geographic region, urban/rural location, teaching status, bed size, and control. The strata that were collapsed for sampling were also collapsed for sample weight calculations. Within stratum s, each NIS sample hospital's universe weight was calculated as:
Ws(universe) = Ns(universe) ÷ Ns(sample),
where Ws(universe) was the hospital universe weight, and Ns(universe) and Ns(sample) were the number of community hospitals within stratum s in the universe and sample, respectively. Thus, each hospital's universe weight (HOSPWT) is equal to the number of universe hospitals it represented during that year. Since 20% of the hospitals in each stratum were sampled when possible, the hospital weights are usually around five.
The calculations for discharge-level sampling weights were similar to the calculations of hospital-level sampling weights. The discharge weights usually are constant for all discharges within a stratum.
The only exceptions were for strata with sample hospitals that, according to the AHA files, were open for the entire year but contributed less than their full year of data to the NIS. For those hospitals, we adjusted the number of observed discharges by a factor of 4 ÷ Q, where Q was the number of calendar quarters for which the hospital contributed discharges to the NIS. For example, when a sample hospital contributed only two quarters of discharge data to the NIS, the adjusted number of discharges was double the observed number. This adjustment was done only for weighting purposes. The NIS dataset only includes the actual (unadjusted) number of observed discharges.
With that minor adjustment, each discharge weight is essentially equal to the number of AHA universe discharges that each sampled discharge represented in its stratum. This calculation was possible because the number of total discharges was available for every hospital in the universe from the AHA files. Each universe hospital's AHA discharge total was calculated as the sum of newborns and hospital discharges.
Discharge weights to the universe were calculated by post-stratification. Hospitals were stratified just as they were for universe hospital weight calculations. Within stratum s, for hospital i, each NIS sample discharge's universe weight was calculated as:
DWis(universe) = [DNs(universe) ÷ ADNs(sample)] * (4 ÷ Qi),
where DWis(universe) was the discharge weight; DNs(universe) was the number of discharges from community hospitals in the universe within stratum s; ADNs(sample) was the number of adjusted discharges from sample hospitals selected for the NIS; and Qi was the number of quarters of discharge data contributed by hospital i to the NIS (usually Qi = 4). Thus, each discharge's weight (DISCWT) is equal to the number of universe discharges it represented in stratum s during that year. Since all discharges from 20% of the hospitals in each stratum were sampled when possible, the discharge weights are usually around five.
In the 10 percent subsamples, each discharge had a 10 percent chance of being drawn. Therefore, the discharge weights contained in the Hospital Weights file can be multiplied by 10 for each of the subsamples, or multiplied by 5 for the two subsamples combined.
It may be important for researchers to calculate a measure of precision for some estimates based on the NIS sample data. Variance estimates must take into account both the sampling design and the form of the statistic. The sampling design was a stratified, single-stage cluster sample. A stratified random sample of hospitals (clusters) were drawn and then all discharges were included from each selected hospital.
If hospitals inside the frame were similar to hospitals outside the frame, the sample hospitals can be treated as if they were randomly selected from the entire universe of hospitals within each stratum. Standard formulas for a stratified, single-stage cluster sampling without replacement could be used to calculate statistics and their variances in most applications.
A multitude of statistics can be estimated from the NIS data. Several computer programs are listed below that calculate statistics and their variances from sample survey data. Some of these programs use general methods of variance calculations (e.g., the jackknife and balanced half-sample replications) that take into account the sampling design. However, it may be desirable to calculate variances using formulas specifically developed for some statistics.
These variance calculations are based on finite-sample theory, which is an appropriate method for obtaining cross-sectional, nationwide estimates of outcomes. According to finite-sample theory, the intent of the estimation process is to obtain estimates that are precise representations of the nationwide population at a specific point in time. In the context of the NIS, any estimates that attempt to accurately describe characteristics (such as expenditure and utilization patterns or hospital market factors) and interrelationships among characteristics of hospitals and discharges during a specific year from 1988 to 1998 should be governed by finite-sample theory.
Alternatively, in the study of hypothetical population outcomes not limited to a specific point in time, analysts may be less interested in specific characteristics from the finite population (and time period) from which the sample was drawn, than they are in hypothetical characteristics of a conceptual "superpopulation" from which any particular finite population in a given year might have been drawn. According to this superpopulation model, the nationwide population in a given year is only a snapshot in time of the possible interrelationships among hospital, market, and discharge characteristics. In a given year, all possible interactions between such characteristics may not have been observed, but analysts may wish to predict or simulate interrelationships that may occur in the future.
Under the finite-population model, the variances of estimates approach zero as the sampling fraction approaches one, since the population is defined at that point in time, and because the estimate is for a characteristic as it existed at the time of sampling. This is in contrast to the superpopulation model, which adopts a stochastic viewpoint rather than a deterministic viewpoint. That is, the nationwide population in a particular year is viewed as a random sample of some underlying superpopulation over time. Different methods are used for calculating variances under the two sample theories. The choice of an appropriate method for calculating variances for nationwide estimates depends on the type of measure and the intent of the estimation process.
The hospital weights will be useful for producing hospital-level statistics for analyses that use the hospital as the unit of analysis, and the discharge weights will be useful for producing discharge-level statistics for analyses that use the discharge as the unit of analysis. The discharge weights would be used to weight the sample data in estimating population statistics.
In most cases, computer programs are readily available to perform these calculations. Several statistical programming packages allow weighted analyses.2 For example, nearly all SAS (Statistical Analysis System) procedures incorporate weights. In addition, several statistical analysis programs have been developed that specifically calculate statistics and their standard errors from survey data. Version 8 of SAS contains procedures (PROC SURVEYMEANS and PROC SURVEYREG) for calculating statistics based on specific sampling designs. Also, OSIRIS IV, developed at the University of Michigan, and SUDAAN, developed at the Research Triangle Institute, do calculations for numerous statistics arising from the stratified, single-stage cluster sampling design. An example of using SUDAAN to calculate variances in the NIS is presented in the report: Calculating Variances Using Data from the HCUP Nationwide Inpatient Sample.3 For an excellent review of programs to calculate statistics from survey data, visit the following website: http://www.hcp.med.harvard.edu/statistics/survey-soft/. ![]()
The NIS database includes a Hospital Weights file with variables required by these programs to calculate finite population statistics. In addition to the sample weights described earlier, hospital identifiers (Primary Sampling Units or PSUs), stratification variables, and stratum-specific totals for the numbers of discharges and hospitals are included so that finite-population corrections (FPCs) can be applied to variance estimates.
In addition to these subroutines, standard errors can be estimated by validation and cross-validation techniques. Given that a very large number of observations will be available for most analyses, it may be feasible to set aside a part of the data for validation purposes. Standard errors and confidence intervals can then be calculated from the validation data.
If the analytical file is too small to set aside a large validation sample, cross-validation techniques may be used. For example, tenfold cross-validation would split the data into ten equal-sized subsets. The estimation would take place in ten iterations. In each iteration, the outcome of interest is predicted for one-tenth of the observations by an estimate based on a model fit to the other nine-tenths of the observations. Unbiased estimates of error variance are then obtained by comparing the actual values to the predicted values obtained in this manner.
Finally, it should be noted that a large array of hospital-level variables are available for the entire universe of hospitals, including those outside the sampling frame. For instance, the variables from the AHA surveys and from the Medicare Cost Reports are available for nearly all hospitals. To the extent that hospital-level outcomes correlate with these variables, they may be used to sharpen regional and nationwide estimates.
As a simple example, each hospital's number of cesarean sections would be correlated with their total number of deliveries. The number of cesarean sections must be obtained from discharge data, but the number of deliveries is available from AHA data. Thus, if a regression can be fit predicting cesarean sections from deliveries based on the NIS data, that regression can then be used to obtain hospital-specific estimates of the number of cesarean sections for all hospitals in the universe.
Hospitals that continue in the NIS for multiple consecutive years are a subset of the hospitals in the NIS for any one of those years. Consequently, longitudinal analyses of hospital-level outcomes may be biased if they are based on any subset of NIS hospitals limited to continuous NIS membership. In particular, such subsets would tend to contain fewer hospitals that opened, closed, split, merged, or changed strata. Further, the sample weights were developed as annual, cross-sectional weights rather than longitudinal weights. Therefore, different weights might be required, depending on the statistical methods employed by the analyst.
One approach to consider in hospital-level longitudinal analyses is to use repeated-measure models that allow hospitals to have missing values for some years. However, the data are not actually missing for some hospitals, such as those that closed during the study period. In any case, the analyses may be more efficient (e.g., produce more precise estimates) if they account for the potential correlation between repeated measures on the same hospital over time, yet incorporate data from all hospitals in the sample during the study period.
The two nonoverlapping 10 percent subsamples of discharges were drawn from the NIS file for each year for several reasons pertaining to data analysis. One reason for creating the subsamples was to reduce processing costs for selected studies that will not require the entire NIS. Another reason is that the two subsamples may be used to validate models and obtain unbiased estimates of standard errors. That is, one subsample may be used to estimate statistical models, and the other subsample may be used to test the fit of those models on new data. This is a very important analytical step, particularly in exploratory studies, where one runs the risk of fitting noise.
For example, it is well known that the percentage of variance explained by a regression, R2, is generally overestimated by the data used to fit a model. The regression model could be estimated from the first subsample and then applied to the second subsample. The squared correlation between the actual and predicted value in the second subsample is an unbiased estimate of the model's true explanatory power when applied to new data.
| Internet Citation: 1998 NIS Design Report. Healthcare Cost and Utilization Project (HCUP). May 2016. Agency for Healthcare Research and Quality, Rockville, MD. hcup-us.ahrq.gov/db/nation/nis/reports/NIS_1998_Design_Report.jsp. |
| Are you having problems viewing or printing pages on this website? |
| If you have comments, suggestions, and/or questions, please contact hcup@ahrq.gov. |
| If you are experiencing issues related to Section 508 accessibility of information on this website, please contact hcup@ahrq.gov. |
| Privacy Notice, Viewers & Players |
| Last modified 5/27/16 |